12.3 Test theory

Test theory is grounded on statistics and the theory of probability. It assumes that the values assigned to the observations (i.e., subjects' responses) constitute a scale. The final goal of test theory is to locate the subjects or the stimuli along a continuum of a non-observable attribute (i.e., a latent trait).

12.3.1 What is a test?

A test is a device or procedure in which a sample of a respondent's behavior in a specified domain is obtained, evaluated, and scored using a standardized process (Standards for Educational and Psychological Tests, 2014). On the one hand, psychological tests include instruments measuring the correctness or quality of the responses (e.g., measures of ability, aptitude). On the other hand, tests are also used to measure attitudes, preferences, and predispositions (e.g., measures of personality, mental health, cognitive functioning, attitudes).

CAUTION!

• There is no unique and universally accepted measure for any given construct. It is required to examine the theoretical framework and its specifications
• All tests are based on limited samples of behavior extracted from the defined population of the domain
• There is always a measurement error (sampling error)
• Absence of scales with origin and unit of measurement (i.e., indetermination of the measurement scale)
• Latent variables cannot be defined in isolation, but by establishing its nomological network with other constructs and observed variables

12.3.2 Classification of psychological tests

• Type of domain: Tests are usually classified as cognitive (e.g., intelligence, ability, academic performance) and non-cognitive tests (e.g., personality, attitudes, motivations, mood). Other authors refer to these two groups of tests as ability (measures of maximum performance) versus personality (measures of typical performance) tests.

• Consequences for the subject: Tests can be placed into a continuum ranging from high- to low-stakes. If the test's scores are used to determine an important outcome (e.g., to get a job, A levels, clinical screening), then it is a high-stakes test.

• Response format/task: The most common response formats range from a selected-response (i.e., the respondent selects the correct, best, or most appropriate response from a list of possible answers to questions or stimuli) to a constructed-response item format (i.e., the respondent produces a written response to a question or stimulus).

• Administration: Tests can be classified according to the administration mode. For example, a psychological test can be administered individually versus collectively, paper-and-pencil versus on-line tests, or adaptive versus non-adaptive tests.

• Response-time constraints: Some psychological tests are classified as speed tests when the items are rather easy but include a time limit. On the other hand, tests classified as power tests are designed to measure the ability of the respondent, not the speed when performing these tests.

• Statistical model: Tests can be classified in relation to the statistical model in which the test scores are based. Classical Test Theory (CTT) is based on the general linear model and test total scores. Item Response Theory (IRT) is based on a nonlinear model estimating the probability to answer to a given item as a function of the different levels of the underlying trait or ability.

• Interpretation of the scores: Some tests focus on the degree of coverage of a certain domain or a predetermined criterion (i.e., criterion-referenced tests). Other tests, however, focus on the relative position of the respondent in relation to a reference group (i.e., norm-referenced tests).

12.3.3 Measurement error

In applied statistics and psychometrics we model data. Models are representations of reality and they do not often fit well into our data. Even in disciplines such as physics, some randomness is expected. Measurement error is pervasive and we need to include it when we model our data. Thus, our data result from adding to the model some measurement error (it is often called residual).

\[\begin{aligned} Data = Model \ + \ Residual\\ \end{aligned}\]

In turn, the measurement error will result from subtracting our model to our data. Put differently, the model is what we know (e.g., the theory X that we used to explain job burnout) and the residual or error is what we still do not know (e.g., what remains unexplained by theory X in relation to the phenomenon of job burnout).

\[\begin{aligned} Residual = Data \ - \ Model\\ \end{aligned}\]

In psychometrics, we assume that any observed score (\(X_{i}\)) is the result of a true score (\(T_{i}\)) plus its measurement error (\(E_{i}\)). Thus, the true score is the quantity that one subject has for a given trait, ability, or attribute. The observed score and the measurement error are random variables, whereas the true score is assumed to be a constant (the score obtained after infinite number of observations on the same subject).

\[\begin{aligned} X_{i} = T_{i} \ + \ E_{i}\\ \end{aligned}\]

There are two sources of error: random error (unsystematic error) and bias (systematic error) (Figure 12.3). In turn, random error decomposes into generic random error and idiosyncratic random error, whereas bias decomposes into additive systematic error and correlational systematic error (Viswanathan, 2005).

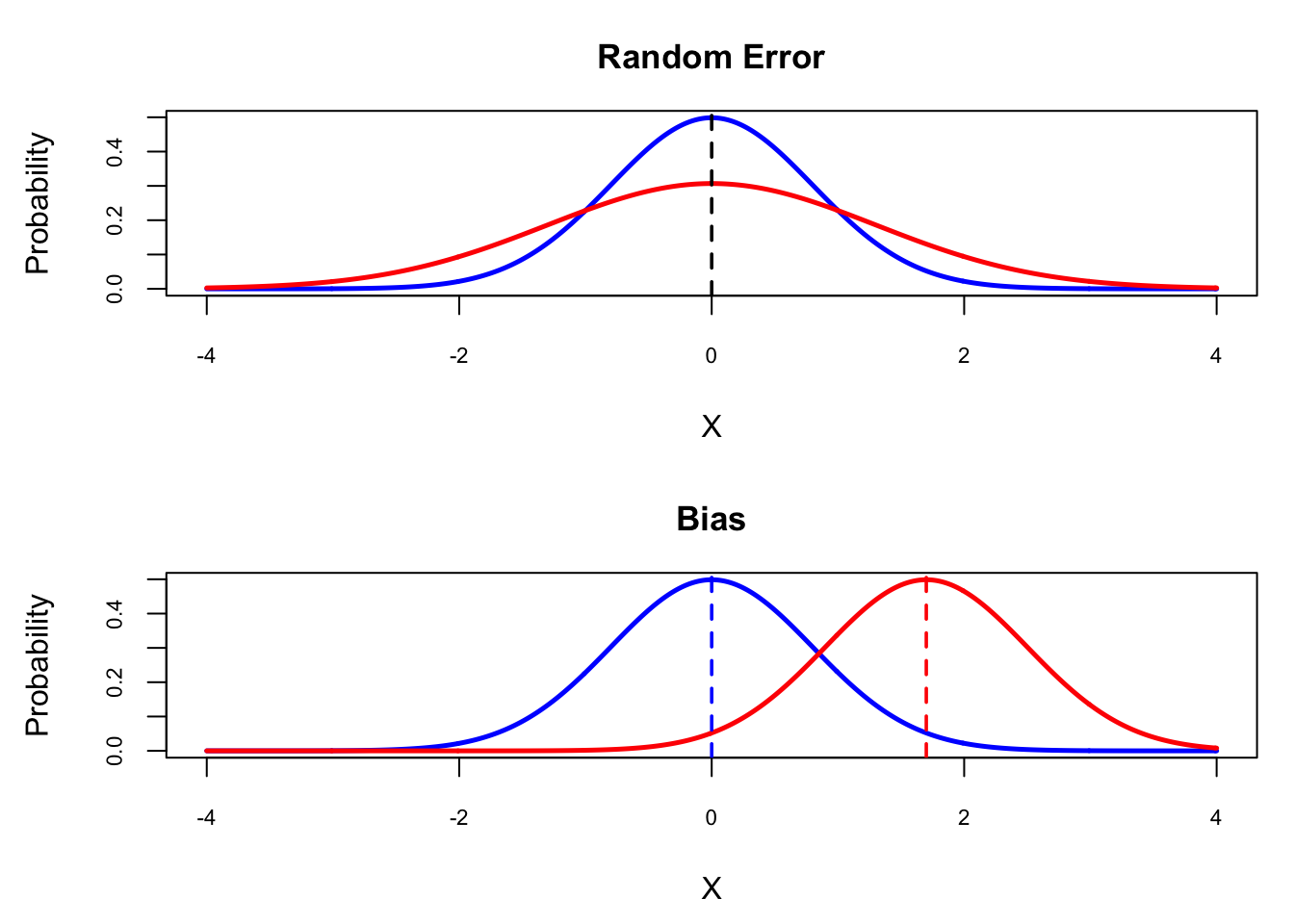
Figure 12.3: Random error (unsystematic error) and bias (systematic error).

12.3.3.1 Random error

It is any type of error that is inconsistent, or it does not repeat in the same magnitude or direction except by chance. This variability in data collection tends to be averaged out in the long run. Sources of random error could be related to ambiguity, unclear wording, or double-barreled questions.

• Idiosyncratic random error: It affects a few subjects (e.g., mood, language comprehension).
• Generic random error: It affects many subjects (e.g., item-wording effects, noisy setting).

12.3.3.2 Bias

It is a type of error that consistently affects our measurements. After taking many repeated measures, this systematic error biases the measurement positively or negatively. Luckily, we can predict this type of error. For example, between the first and the second administration of a test, maturation, learning, or fatigue might explain the bias.

• Additive systematic error: It increases or decreases the observed values by a constant magnitude (e.g., leading questions).
• Correlational systematic error: It increases or decreases the relationship between variables (e.g., some subjects might interpret the response categories in some way, whereas other subjects might interpret these categories in a different way).